728x90
반응형
📌 깊이 우선 탐색이란?
- 그래프 탐색 기법
- 그래프 완전 탐색 기법 중 하나
- 그래프의 시작 노드에서 출발하여 하나의 분기를 정해 최대 깊이까지 탐색
- 이후, 탐색하지 않은 다른 분기로 이동해 탐색을 수행
- 구현 방식
- 재귀 함수나 스택을 사용해서 구현
- 각 노드의 방문 여부를 기록하여 중복 탐색을 방지
- 탐색 순서
- 깊이를 우선으로 탐색하기 때문에 한 방향으로 끝까지 탐색한 뒤 다시 되돌온다.
- 미로 탐색 시, 한 방향으로 갈 수 있을 때까지 이동하다 막다른 길에 도달하면 이전 갈림길로 돌아가 다른 방향으로 탐색하는 과정과 유사하다.
- 단순하지만 강력한 알고리즘
- DFS는 너비 우선 탐색(BFS)에 비해 상대적으로 구현이 간단함
- 단순 검색 속도는 BFS보다 느릴 수 있으며, 경우에 따라 무한루프에 빠질 가능성도 있으므로 방문 기록이 중요함
🔍 DFS의 주요 특징
- 재귀 함수로 구현 가능
- DFS는 함수 호출 스택을 활용하여 직관적으로 구현 가능
- 재귀 호출이 많아질 경우 스택 오버플로(stack overflow)에 주의해야 함
- 스택 자료 구조 활용
- 재귀 대신 반복문 기반의 DFS 구현 가능
- 시간 복잡도
- DFS의 시간 복잡도: O(V + E)
- V: 그래프의 노드 수
- E: 그래프의 간선(edge) 수
- 그래프의 모든 노드와 간선을 한 번씩 탐색하기 때문에 효율적
- DFS의 시간 복잡도: O(V + E)
- 방문 여부 확인 필수
- 무한 루프 방지를 위해 각 노드의 방문 여부를 반드시 기록해야 함
🔧 DFS의 활용과 문제 유형
- 단절점(Articulation Point) 찾기
- 그래프에서 특정 노드를 제거했을 때, 연결 요소의 개수가 증가하는 노드 찾기.
- 단절선(Bridge) 찾기
- 특정 간선을 제거했을 때, 그래프가 분리되는 간선 탐색.
- 사이클(Cycle) 찾기
- 그래프 내에서 사이클(순환 구조)을 찾는 문제 해결.
- 위상 정렬(Topological Sort)
- 방향성이 있는 비순환 그래프(DAG)에서 노드의 순서를 정하는 문제.
- DFS를 활용해 위상 정렬을 수행할 수 있습니다.
🚫 DFS 사용 시 주의할 점
- 스택 오버플로
- 재귀 호출이 많아질 경우, 스택 메모리가 초과될 수 있음
➡️ 재귀 대신 스택을 사용하거나, 그래프 크기를 고려한 메모리 관리를 해야 함
- 재귀 호출이 많아질 경우, 스택 메모리가 초과될 수 있음
- 그래프 표현 방식
- DFS는 인접 리스트로 구현할 때 더욱 효율적
- 인접 행렬은 공간 복잡도가 높으므로 적합하지 않을 수 있음
🚀 DFS와 BFS 비교
| 특징 | DFS | BFS |
| 탐색 방식 | 한 분기를 최대 깊이까지 탐색 후 복귀 | 가까운 노드부터 탐색 |
| 구현 복잡도 | 간단함(재귀/Stack 활용) | 상대적으로 복잡함(Queue 활용) |
| 속도 | 느릴 수 있음 | 단순 검색 속도는 더 빠름 |
| 메모리 사용량 | 적음 | 상대적으로 많음 |
| 적합한 경우 | 모든 경로를 확인해야 하는 경우 | 최단 경로를 탐색해야 하는 경우 |
🥐 깊이 우선 탐색 과정
1️⃣ DFS 준비 단계
- 시작 노드 선택
- 탐색을 시작할 노드를 선택합니다.
- 자료구조 초기화
- 인접 리스트로 그래프를 표현하여 탐색 경로를 효율적으로 관리합니다.
- 방문 배열을 초기화하여 각 노드의 방문 여부를 기록합니다.
- 시작 노드를 스택에 삽입하고, 방문 배열에서 해당 노드를 True로 설정합니다.
2️⃣ 탐색 과정 (반복)
- 스택에서 노드 꺼내기
- 스택에서 노드를 꺼내 탐색 순서에 기록합니다.
- 꺼낸 노드의 인접 리스트를 확인하여 연결된 노드를 처리합니다.
- 인접 노드 탐색
- 방문하지 않은 인접 노드만 스택에 삽입하고 방문 배열을 업데이트합니다.
- 이미 방문한 노드는 재삽입하지 않음이 핵심입니다.
3️⃣ 종료 조건
- 스택이 빌 때까지 위 과정을 반복합니다.
- 모든 노드가 탐색되면 종료합니다.
💡 DFS 동작 방식 예제
1️⃣ DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
<초기 작업>
- 인접 리스트로 그래프 표현하기
- 방문 배열 초기화하기
- 시작 노드 스택에 삽입하기

스택 초기 상태
- 시작 노드 1 삽입: 스택 [1]
- 방문 배열: T, F, F, F, F, F
2️⃣ 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기

스택에서 1 꺼내기
- 1의 인접 노드 2, 3 중 3부터 삽입: 스택 [3, 2]
- 방문 배열: T, T, T, F, F, F
3️⃣ 스택 자료구조에 값이 없을 때까지 반복하기
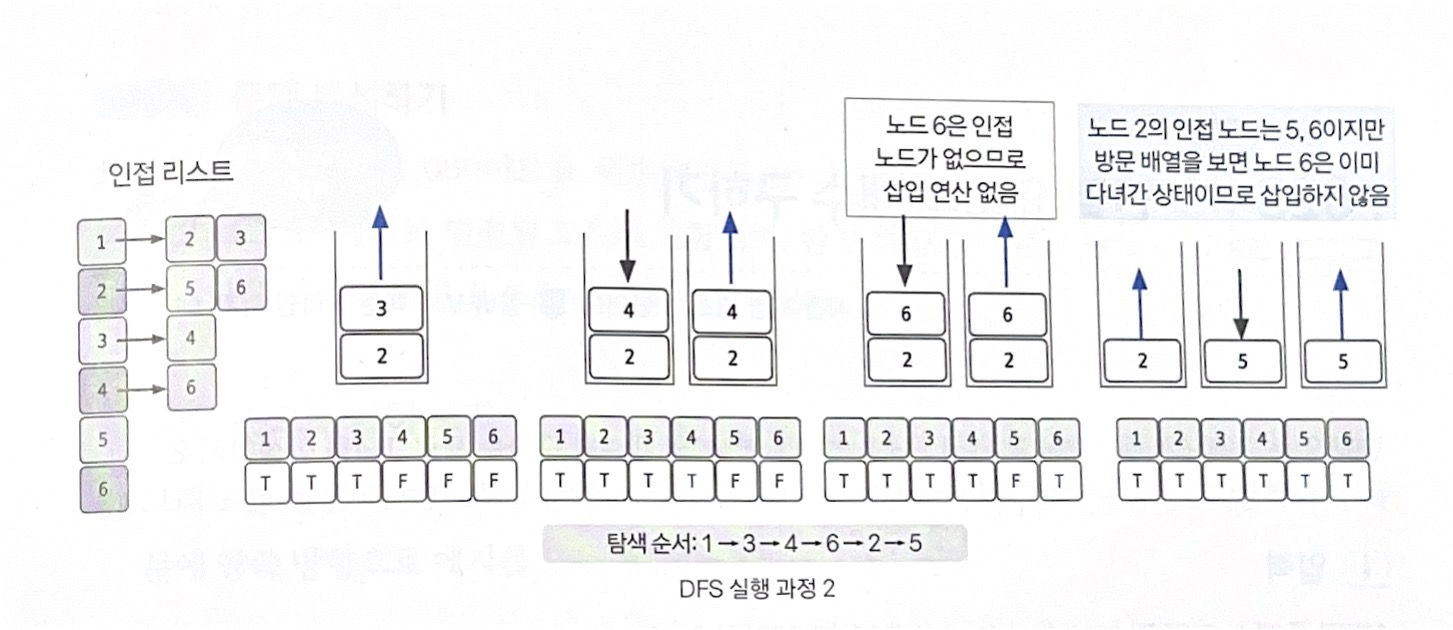
🚨이미 다녀간 노드는 방문 배열을 바탕으로 재삽입하지 않는 것이 핵심 ❗️
- 스택에서 3 꺼내기
- 3의 인접 노드 4 삽입: 스택 [4, 2]
- 방문 배열: T, T, T, T, F, F
- 스택에서 4 꺼내기
- 4의 인접 노드 6 삽입: 스택 [6, 2]
- 방문 배열: T, T, T, T, F, T
- 스택에서 6 꺼내기
- 6에 인접 노드가 없으므로 탐색 순서에 기록만 함.
- 스택에서 2 꺼내기
- 2의 인접 노드 5 삽입: 스택 [5]
- 방문 배열: T, T, T, T, T, T
- 스택에서 5 꺼내기
- 5에 인접 노드가 없으므로 종료.
✅ 핵심 포인트
- 막다른 길 처리: 더 이상 진행할 수 없으면 스택에서 이전 경로로 돌아감.
- 방문 배열 활용: 이미 방문한 노드는 재삽입하지 않음으로써 불필요한 탐색을 방지.
- 스택의 후입 선출 특성: 최신에 추가된 노드부터 처리하여 깊이 우선 탐색 구현.
✅ 다음 게시글에서 예제 문제로 더 자세히 이해해보도록 하겠습니다!
[JAVA][Baekjoon] 10989번 수 정렬하기 3
https://www.acmicpc.net/problem/11724📌 접근 방식1️⃣ 접근 방식 그래프의 표현입력된 정점과 간선 정보는 인접 리스트를 사용하여 그래프 표현인접 리스트 : 정점마다 연결된 다른 정점들의 목록을
nyeroni.tistory.com
[JAVA][Baekjoon] 2023번 신기한 소수
https://www.acmicpc.net/problem/2023📌 접근 방식DFS(깊이 우선 탐색) 을 사용했다! 한 자리씩 숫자를 추가하면서 신기한 소수를 탐색하기에 적합하기 때문숫자를 추가할 때마다 소수인지 확인하고, 조
nyeroni.tistory.com
Reference
[알고리즘] 깊이 우선 탐색(DFS)이란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
728x90
반응형
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 이진 탐색(Binary Search) (0) | 2025.01.06 |
|---|---|
| [알고리즘] 너비 우선 탐색 : BFS(Breadth-First-Search) (0) | 2025.01.06 |
| [알고리즘] 기수 정렬(Radix Sort)이란? (0) | 2025.01.03 |
| [알고리즘] 병합 정렬(Merge Sort)이란? (0) | 2025.01.03 |
| [알고리즘] 퀵 정렬(Quick Sort)이란? (1) | 2025.01.02 |